Question

You make some iced tea by dropping 325 grams of ice into 500.0 mL of warm tea in an insulated pitcher. If the tea is initially at 30.0°C and the ice cubes are initially at 0.0°C, how many grams of ice will still be present when the contents of the pitcher reach a final temperature? The tea is mostly water, so assume that it has the same density (1.0 g/mL), molar mass, heat capacity (75.3 J/K/mol), and heat of fusion (6.01 kJ/mol) as pure water. The heat capacity of ice is 37.7 J/K/mol.

Answer 1

Step-by-step explanation:

The given data is as follows.

Mass of ice dropped = 325 g

Initial temperature =
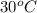`30^(o)C` = (30 + 273) K = 303 K

Final temperature =
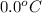`0.0^(o)C` = (0 + 273) K = 273 K

Now, using density of water calculate the mass of ice as follows.

`m_(ice) = (500 ml * 1.0 g/mol)/(1 ml)`

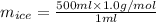
= 500 g

As the relation between heat energy, specific heat and change in temperature is as follows.

Q =
`m * C_(p) * dT`

=
`(500 g)/(18 g/mol) * 75.3 J/K/mol * (303 - 273)K`

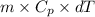
= 62750 J

Also, relation between heat energy and latent heat of fusion is as follows.

Q = m L

=
`(325 g)/(18 g/mol) * 6 * 10^(3)`

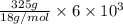
= 108300 J

Therefore, we require
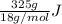`(325 g)/(18 g/mol) J` heat but we have 40774.95 J.

So,
`mass_(ice) = (m * C_(p) * (T_(f) - T_(i)))/(\Delta H_(f))`

=
`(62750 J)/(333)`

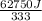
= 188.4 g

Hence, the mass of ice = 325 g - 188.4 g

= 137 g

Therefore, we can conclude that 137 g of ice will still be present when the contents of the pitcher reach a final temperature.