Answer:
The pairs of integer having two real solution for
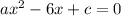 are
are




Explanation:
Given
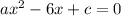
Now we will solve the equation by putting all the 6 pairs so we get the following
 for
for
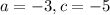
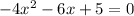 for
for

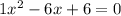 for
for

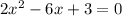 for
for
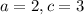
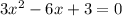 for
for
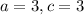
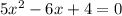 for
for
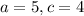
The above all are Quadratic equations inn general form

where we have a,b and c constant values
So for a real Solution we must have

for
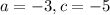 we have
we have
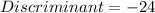 which is less than 0 ∴ not a real solution.
which is less than 0 ∴ not a real solution.
for
 we have
we have
 which is greater than 0 ∴ a real solution.
which is greater than 0 ∴ a real solution.
for
 we have
we have
 which is greater than 0 ∴ a real solution.
which is greater than 0 ∴ a real solution.
for
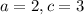 we have
we have
 which is greater than 0 ∴ a real solution.
which is greater than 0 ∴ a real solution.
for
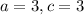 we have
we have
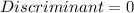 which is equal to 0 ∴ a real solution.
which is equal to 0 ∴ a real solution.
for
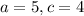 we have
we have
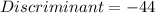 which is less than 0 ∴ not a real solution.
which is less than 0 ∴ not a real solution.