Answer:
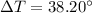
Step-by-step explanation:
It is given that,
Mass of the car, m = 763 kg
Speed of the car, v = 26 m/s
Mass of the iron, m' = 15 kg
Specific heat of iron, c = 450 J/kg
When the car is in motion, it will possess kinetic energy. It is given by :
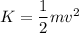
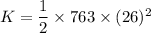
K = 257894 J
Since, energy is absorbed by the brakes. The kinetic energy of the car is absorbed by the brakes. So,
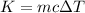
 is the increase in temperature of the brakes
is the increase in temperature of the brakes
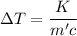
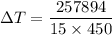
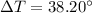
So, the increase in temperature of the brakes is 38.20 degrees Celsius. Hence, this is the required solution.