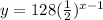Question

Arianna is participating in a tennis tournament that begins with 128 players. After each round, half of the remaining players advance to the next round of the tournament. Which function relates the number of rounds played, x, and the number of players advancing to the next round?

Answer 1

128(1/2)^x

Explanation:

Answer 2

`y=128((1)/(2) )^(x-1)`

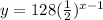
Explanation:

This problem models a geomatric sequence, because each new element is half of the last one.

A geometric sequence is defined as

`a_(n)=a_(1)r^(n-1)`

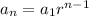
Where
`n` is the position of the element,
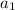`a_(1)` is the first element and
`r` is the reason that creates the sequence.

In this case, we have

`a_(1)=128`,
`r=(1)/(2)`

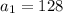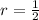
Replacing this values, we have

`a_(n) =128((1)/(2))^(n-1)`

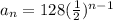
Where
`n` is the independent variable and
`a_(n)` is the dependent variable.

Therefore, the function that relates the number of rounds and the number of players advaincing to the next round is

`y=128((1)/(2) )^(x-1)`