Answer:
The autoclave must operate at 1.94 atm pressure.
Step-by-step explanation:
To calculate
 of the reaction, we use Clausius Clapeyron equation, which is:
of the reaction, we use Clausius Clapeyron equation, which is:
![\ln((P_2)/(P_1))=(\Delta H_(vap))/(R)[(1)/(T_1)-(1)/(T_2)]](https://img.qammunity.org/2020/formulas/chemistry/college/4vtbgz8qequ3vvsclhkmmvxlsikmj2gcnu.png)
where,
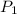 = Pressure of autoclave at temperature
= Pressure of autoclave at temperature
 = 1 atm
= 1 atm
 = Pressure of autoclave at temperature
= Pressure of autoclave at temperature
 = ?
= ?
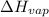 = Enthalpy of vaporization = 40.656 kJ/mol = 40,656 J/mol
= Enthalpy of vaporization = 40.656 kJ/mol = 40,656 J/mol
R = Gas constant = 8.314 J/mol K
 = initial temperature =
= initial temperature =
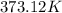
 = final temperature =
= final temperature =
![120^oC=[120+273.15]K=393.15 K](https://img.qammunity.org/2020/formulas/chemistry/college/r83ipqhk1pmxzgjmc9q2o5nu8raqxachhi.png)
Putting values in above equation, we get:
![\ln((P_2)/(1 atm))=(40,656 J/mol)/(8.314J/mol.K)[(1)/(373.12 K)-(1)/(393.15 K)]\\\\ P_2=1.94 atm](https://img.qammunity.org/2020/formulas/chemistry/college/ech3hsblpu3zqzevmx3rx3dpd6d7bqu2u9.png)
The autoclave must operate at 1.94 atm pressure.