Question

Find the maximum value of the funtion z=4x+3y subject the following constraints.

3x+2y≤20
x≥2
x≤6
y≥0
Label each vertex

Answer 1

The gradient of this function is

`\left((\partial z)/(\partial x),(\partial z)/(\partial y)\right)=(4, 3)`

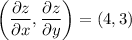
So, it is never zero, and the function has no absolute maximum/minimum points (after all, it's a plane...)

So, we evaluate the function along the borders of our domain, and look for the maximum value there. The domain is the trapezium with vertices

`A=(2, 0),\ B=(6, 0),\ C=(6, 1),\ D=(2, 7)`

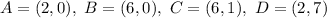
If we go along AB, y is constantly 0, and x increases from 2 to 6. So, the maximum value for
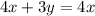`4x+3y=4x` is 4*6=24

If we go along BC, x is constantly 6, and y increases from 0 to 1. So, the maximum value for
`4x+3y=24+3y` is 24+3*1=27

If we go along AD, x is constantly 2, and y increases from 0 to 7. So, the maximum value for
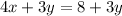`4x+3y=8+3y` is 8+3*7=29

Finally, if we go along CD, y is -3/2x+10, and x ranges from 2 to 6. Since the line is descending, it has its maximum value at x=2, and we have point D again.

So, the maximum is 29, at (2,7).