Question

A pop-quiz has five multiple choices questions, each with choices: A , B , C or D . I didn't study for this quiz and decided circle the answers at random. What is the probability that I will get exactly four of the five questions right?

Answer 1

Answer: The required probability is 1.46%.

Step-by-step explanation: Given that a pop-quiz has five multiple choices questions, each with choices: A , B , C or D . We decided to circle the answers at random.

We are to find the probability that we will get exactly four of the five questions right.

Since we have only two results, correct and incorrect for each question, so this is a case of Binomial Distribution.

We know that

the probability of r success in number of trials is given by

`P(X=r)=^nC_rp^rq^(n-r).`

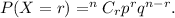
Since we have four options for a question, out of which one is correct, we have

`p=\textup{Probability of success}=(1)/(4),\\\\\\q=\textup{Probability of failure}=1-p=1-(1)/(4)=(3)/(4).`

Therefore, the probability getting four questions correct out of 5 is

`P(X=4)\\\\\\=^5C_4\left((1)/(4)\right)^4\left((3)/(4)\right)^1\\\\\\=5*(1)/(256)*(3)/(4)\\\\\\=(15)/(1024)\\\\=0.0146\\\\1.46\%.`

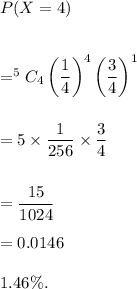
Thus, the required probability is 1.46%.