Answer:
7 miles per hour
Explanation:
Data:
Rate of current = 5 miles / hr
The solution to this problem is in two parts:
1) Rowing team going with the current covering 60 miles
2) Rowing team going against the current covering 10 miles
The formula used to calculate rate will be :
Velocity =
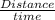 = v =
= v =
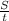
1) Rowing team going with the current covering 60 miles
Distance = S = 60 miles
Rate = velocity = Rate of Current + Rate of rowing team =
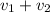 = 5 +
= 5 +
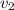
using the velocity formula:
5 +
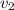 =
=
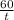 --------------------- Equation. 1
--------------------- Equation. 1
2) Rowing team going against the current covering 10 miles
Distance = S = 10 miles
As the current is against the direction of rowing team so the rate of current will be subtracted from the rate of rowing team.
Rate = velocity = Rate of rowing team - Rate of Current =
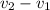 =
=
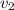 - 5
- 5
Using velocity formula:
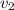 - 5 =
- 5 =

Cross multiplying
t = (10) ÷ (
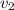 - 5)
- 5)
put this in equation 1.
we get :
5 +
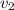 = (
= (
 )
)
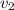 - 5
- 5
5 +
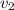 = (6)
= (6)
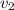 - 5
- 5
5 +
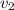 =
=
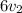 - 30
- 30
5 + 30 =
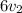 -
-
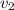
35 =
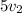
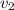 =
=

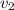 = 7 miles/hr
= 7 miles/hr
rate of the rowing team boat in still water=7 miles/hr