Answer:
The oldest brother is of age
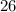 years.
years.
Explanation:
As the age of four brothers are consecutive even integers.
We assume that the ages are
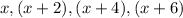 as their respective ages.
as their respective ages.
And the age of the youngest brother
 yrs.
yrs.
Age of the oldest brother
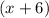 yrs.
yrs.
According to the question
Product of two middle brother that is
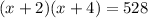
So we will arrange this in our equation and solve the quadratic.
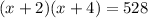
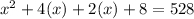
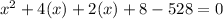

Solving the quadratic by using middle term splitting or directly with quadratic formula we can find the value of 'x' .
Here it is solved with quadratic formula:
Comparing with standard equation
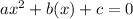 ,here
,here
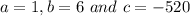 .
.
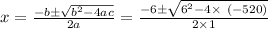
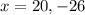
We will work with the positive value of (x) so the the age of the youngest brother
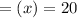 yrs.
yrs.
And the age of the the oldest brother
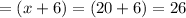 years.
years.
The age difference is of
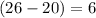 years.
years.