Answer:
Work done, W = 255.21 J
Step-by-step explanation:
It is given that,
Rotational inertia of the wheel,
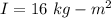
Angular displacement,
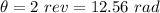
Initial angular velocity,

Final angular velocity,
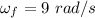
Firstly finding the angular acceleration of the wheel using the equation of rotational kinematics as :
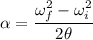
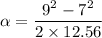
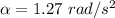
Work done by the torque is given by :
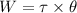
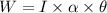
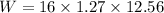
W = 255.21 J
Out of given options, the correct option for the work done by the torque is 255.21 J. Hence, this is the required solution.