Question

A 964-kg car starts from rest at the bottom of a drive way and has a speed of 3.00 m/s at a point where the drive way has risen a vertical height of 0.600 m. Friction and the drive force produced by the engine are the only two non conservative forces present. Friction does -2870 J of work. How much work does the engine do?

Answer 1

Work done by the engine is 12876.32 joules.

Step-by-step explanation:

We know that,

`\mathrm{W}=\mathrm{KE}+\mathrm{PE}+\mathrm{W}_{\mathrm{f}}`

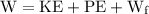
Where,

W = work done by engine

`\mathrm{KE}=\mathrm{kinetic} \text { energy at top of driveway }=(1)/(2)\left(\mathrm{mV}^(2)\right)`

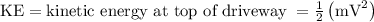
m = mass of the car = 964kg.

V = speed of car at top of driveway = 3 m/sec

PE = potential energy at top of driveway = m × g × h

`\mathrm{g}=\text { acceleration due to gravity }=9.8 \mathrm{m} / \mathrm{s}^(2)`

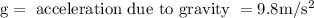
h = vertical height of driveway = 0.6 m

`\mathrm{W}_{\mathrm{t}}=\text { work done against friction }=2870`

Substituting values,

`W=(1)/(2) *(964) *\left(3^(2)\right)+964 *(9.8) *(0.6)+2870`

`W=0.5 * 964 * 9+964 * 9.8 * 0.6+2870`

`\mathrm{W}=4338+5668.32+2870`

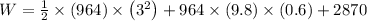
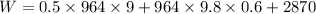
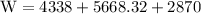
W = 12876.32 joules

Work done by the engine is 12876.32 joules.