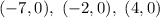Question

A function is defined as a relation for which each x-value has exactly one corresponding y-value. The graph of a function, f(x) is shown below.

Use the graph of the function, f(x), to complete each statement. Enter numerical answers into the spaces provided.

1.f(0)=_____
2.f(2)=_____
3.For the function,f(x), there are exactly three x-values for which the corresponding y-value is zero. In ascending order,f(x), whenx=_____, ______, and______
4.f(-8)=______
5.f(-6)=_______

Answer 1

f(x) = -1 (x - 3)(x + 4)

Explanation:

First one is -1, Second one is 3, And the last one is 4

Answer 2

If you want to evaluate a function
`f` at a specific point
`k`, you'll have to look for
`k` on the x axis, and then look vertically for the point on the graph.

The y coordinate of that point is the corresponding y value.

So, for example, if we want
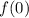`f(0)`, we start from the origin and go up, until we find the point
`(0,1)` that belongs to the graph. So, we have
`f(0)=1`.

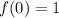Similarly, for
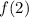`f(2)`, we start from 2 on the x axis and go up until we meet the point
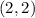`(2, 2)` on the graph. So, we have
`f(2)=2`.

For
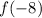`f(-8)`, we start from -8 on the x axis and go up until we meet the point
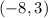`(-8, 3)` on the graph. So, we have
`f(-8)=3`.

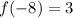For
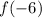`f(-6)`, we start from -6 on the x axis and go down until we meet the point
`(-6, -3)` on the graph. So, we have
`f(-6)=-3`.

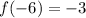The three x-values for which the corresponding y-value is zero are the x-coordinates of the points where the graph crosses the x axis (this means that the y axis is zero). Those three points are
`(-7, 0),\ (-2, 0),\ (4, 0)`