Answer: 73,57%.
Step-by-step explanation:
We need to find P(Z > 24.8)
To answer this question, we use the central limit theorem.
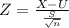
Where:
- X = Sample mean
- U = Population mean
- S = Population standard deviation
- n = sample size
Hence, replacing
Z =
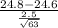
Z = 0.63
We look up 0.63 on the normal distribution table, and we obtain 0.7357
Therefore, the probability that in a radom sample of 63 men, the mean marriage age is less than 24.8 years is 73,57%.