Question

GEOMETRY HELP im BEING TIMED

Answer 1

Part 1: x = 6.2

Part 2: u = 3.46 and v = 2

Part 3: Altitude = 5.196

Explanation:

Part 1:

From the given figure, we can write

`\cos 59 = (x)/(12)`

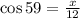
⇒ x = 12 cos 59 = 6.18 ≈ 6.2 (Answer)

Part 2:

From the figure we can write
`\sin 60 = (u)/(4)`

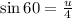
⇒ u = 4 sin 60 = 3.46 (Answer)

And
`\cos 60 = (v)/(4)`

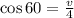
⇒ v = 4 cos 60 = 2 (Answer)

Part 3:

Perimeter of the equilateral triangle is 18.

So, if each side is a, then 3a = 18

⇒ a = 6

Now, if we draw an altitude to the equilateral triangle then it will bisect the base perpendicularly.

If the altitude is x,

Therefore, applying Pythagoras Theorem we get

x² + 3² = 6²

⇒ x² = 27

⇒ x = 5.169 (Answer)