Question

The sum of a rational number and an irrational number?

A. Is a rational number
B. Is undefined
C. Is a rational number
D. Cannot be determined without more information

Answer 1

Is irrational

Explanation:

Let
`r` be a rational number, and
`i` be an irrational number. If their sum were rational, say
`q`, then we'd have

`r+i=q \iff i=q-r`

but
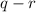`q-r` is the difference between two rational numbers, and thus a rational number. But it also equals
`i`, which is irrational by hypothesis. Since we have a contradiction, we conclude that the sum of a rational and an irrational can't be rational.