Answer:
Diameter, d = 95.7 cm
Step-by-step explanation:
It is given that,
Angular separation of the two components of a double star is,
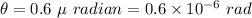
Wavelength of double star,
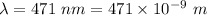
Let d is the diameter of the smallest telescope mirror that will resolve the double star. The formula for the angular separation is given by :
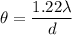
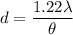
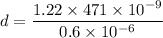
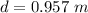
or
d = 95.7 cm
So, the diameter of the smallest telescope mirror that will resolve the double star is 95.7 cm. Hence, this is the required solution.