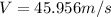Answer: 45.95 m/s
Step-by-step explanation:
When we talk about circular motion, the object's acceleration
 (which is a vector quantity) has two components: the centripetal acceleration
(which is a vector quantity) has two components: the centripetal acceleration
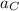 always directed to the center of the circular track and the tangential acceleration
always directed to the center of the circular track and the tangential acceleration
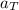 which is tangent to the circular path.
which is tangent to the circular path.
Since both vectors are perpendicular to each other, the magnitude of
 can be calculated by the Pithagorean Theorem:
can be calculated by the Pithagorean Theorem:
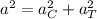 (1)
(1)
Where:
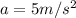
 where
where
 is the speed and
is the speed and
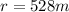 is the radius of the circle
is the radius of the circle
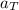 can be calculated knowing the initial speed (
can be calculated knowing the initial speed (
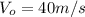 ) and final speed (
) and final speed (
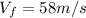 ) of the car and the time (
) of the car and the time (
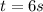 ) it takes to accelerate at this constant rate:
) it takes to accelerate at this constant rate:

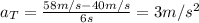
Rewritting (1):
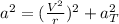 (2)
(2)
Isolating
 :
:
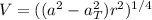 (3)
(3)
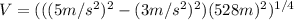 (4)
(4)
Finally: