Question

The decay of the isotope iodine-131 is first-order with a rate constant of 0.138 d−1. All radioactive decay is first order. How many days will it take for 90% of the isotope to decay to Xe-131?

Answer 1

16.7 days

Step-by-step explanation:

We are given;

A radioactive isotope Iodine-131`

The decay rate is 0.138 d⁻¹

The percent decayed is 90%

We are suppose to calculate the number of days for the decay.

• Using the formula;

`In(([A_(0)])/([A]))=kt`

Where,
`[A_(0)]` is the initial concentration and
`[A]` is the new concentration.

• Rearranging the formula;

`t=In(([A_(0)])/([A]))/k`

Assuming the initial concentration is x, then the final concentration after 90% decay will be 0.10x

Therefore;

`t=In(([x])/([0.10x]))((1)/(0.138))`

`t=In(([1])/([0.10]))((1)/(0.138))`

`t=In(10.0)((1)/(0.138))`

`t=(2.3026)((1)/(0.138))`

`t=16.685`

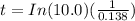
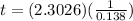
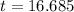
Time = 16.7 days

Therefore, it will take 16.7 days for 90% of I-131 to decay to Xe-131