Question

Y = floor(x)-x+2

From the graph, it is periodic. But how to prove it?

Answer 1

It is sufficient to prove that
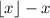`\lfloor x\rfloor-x` is periodic. We claim that the period is 1, and here's the proof:

Let

`f(x)=\lfloor x\rfloor-x`

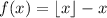
by definition of periodic function, we are claiming that, for every value of x,

`f(x+1)=f(x) \iff \lfloor x+1\rfloor-(x+1)=\lfloor x\rfloor-x`

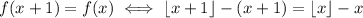
The floor is additive with integers: if a is a real number and b is an integer, we have

`\lfloor a+b\rfloor=\lfloor a\rfloor+\lfloor b\rfloor`

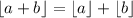
So, we have

`f(x+1)=\lfloor x+1\rfloor-x-1=\lfloor x\rfloor+\lfloor1\rfloor-x-1=\lfloor x\rfloor+1-x-1=\lfloor x\rfloor-x=f(x)`

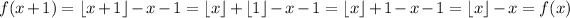
Which proves that the function is periodic with period 1. The idea is that
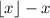`\lfloor x\rfloor-x` is the decimal part of x. For example, if you start at x=2.5 you have

`\lfloor 2.5\rfloor -2.5=2-2.5=-0.5`

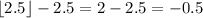
If you go one period ahead, i.e. if you add 1, you have

`\lfloor 3.5\rfloor -3.5=3-3.5=-0.5`

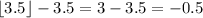
And as you can see, the integer part doesn't matter, because you'll always have a difference in the form

xx - xx.5 = -0.5