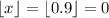Answer:
No
Explanation:
A periodic function has a period T such that, for every x, we have
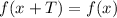
In this case, it would mean that there exists a number T such that, for every x,
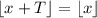
but we can always choose a value for x that is near enough (i.e. less than T) an integer. For example, if T=0.2, we can choose x=0.9 (which is 0.1 away from the next integer, which is less than 0.2).
This choice implies that
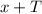 and
and
 don't share the same integer part, and thus their floor is different:
don't share the same integer part, and thus their floor is different:
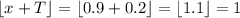
whereas