Question

ABCD is a trapezium with AB= x cm, DC=( x+ 4 )cm and the distance between the parallel sides AB and DC is 1/2 x cm

(a)- Find and simplify, an expression in terms of x for the area of the trapezium.
The area of the Trapezium is 84 cm2





(b)- Calculate the value of x

Answer 1

We know that the smaller base is x cm, the greater base is x+4 cm, and that the height is x/2 cm.

Since the area of a trapezium is given by

`A=((b+B)h)/(2)`

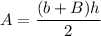
If we plug the expressions we have

`A=((x+(x+4))(x)/(2))/(2)=((2x+4)x)/(4)=(2x^2+4x)/(4)`

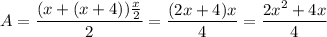
If this must equal 84, we can solve for x as follows: start with

`(2x^2+4x)/(4)=84`

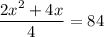
Multiply both sides by 4:

`2x^2+4x=336`

Subtract 336 from both sides:

`2x^2+4x-336=0`

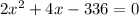
We can divide both sides by 2 to make computation simpler:

`x^2+2x-168=0`

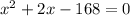
Use the quadratic formula (or any mean you prefer) to solve this equation and get the solutions

`x_1=-14,\quad x_2=12`

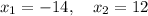
We can't accept the negative solution, because it would imply

`AB=-14,\quad CD=-10`

and we can't have negative side lengths. So, the answer is 12.