The ratio between the masses of Jupiter and Venus is

We can separate the coefficient and the powers of ten:
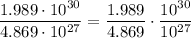
Use the exponent rule

to simplify the powers of 10:
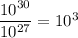
So, the ratio is
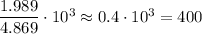
So, Jupiter has a mass that is approximately 400 times greater than Venus's.