Question

Complete the square to rewrite y = x2 - 6x + 15 in vertex form. Then state

whether the vertex is a maximum or minimum and give its coordinates.

A. Maximum at (-3,6)
B. Maximum at (3,6)
C. Minimum at (3,6)
D. Minimum at (-3,6)

Answer 1

Minimum at (3, 6)

Explanation:

its right

Answer 2

Since
`x^2` is the square of x and 6x is twice the product between x and 3, the second square must be 3 squared, i.e. 9.

So, if we think of 15 as 9+6, we have

`x^2-6x+9+6 = (x-3)^2+6`

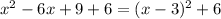
Which is the required vertex form. This form tells us imediately that the vertex is the point (3,6).

Since the leading coefficient is 1, the parabola is facing upwards (it's U shaped), so the vertex is a minimum.