Question

Find all solutions of the equation in the interval [0, 2pi) tan^2(x)=sec(x)-1

Answer 1

Rewrite the equation recalling the definitions of secant and tangent:

`(\sin^2(x))/(\cos^2(x))=(1)/(\cos(x))-1`

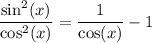
Rearrange the right hand side:

`(\sin^2(x))/(\cos^2(x))=(1-\cos(x))/(\cos(x))`

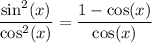
Multiply both sides by cos^2(x):

`\sin^2(x)=\cos(x)-\cos^2(x)`

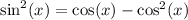
Use the fundamental equation of trigonometry to express
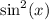`\sin^2(x)` in terms of
`\cos^2(x)`:

`\cos^2(x)+\sin^2(x)=1 \iff \sin^2(x)=1-\cos^2(x)`

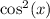So, the expression becomes

`1-\cos^2(x)=\cos(x)-\cos^2(x)`

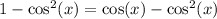
Simplifiy
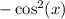`-\cos^2(x)` from both sides:

`1=\cos(x)`

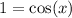
Which only happens if x=0.