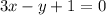The line equation that passes through the given points is
SOLUTION:
Given, two points are A(-1, -2) and B(3, 10).
We need to find the line equation that passes through the given two points. We know that, general equation of a line passing through two points
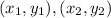 is given by
is given by
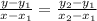
This can be written as,
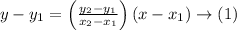
here, in our problem
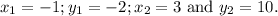
Now substitute the values in (1)

Hence, the line equation that passes through the given points is