Question

The function h(t) = −16t2 + 24t models the height, in feet, of a kangaroo t seconds after it jumps. What is the maximum height of the jump?

Answer 1

9 ft

Explanation:

The height of kangaroo after it jumps is represented by the function
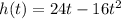`h(t)=24t-16t^(2)`, where
`t` is in seconds, height is in feet.

To find the maximum height that the kangaroo jumps, we need to maximise
`h(t)`.

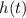The minimum/maximum value of a quadratic expression
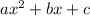`ax^(2)+bx+c` is given by
`(4ac-b^(2))/(4a)`.

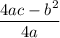As the coeffecient of quadratic term is negative, the function has a maxima.

Maximum value =
`(4(-16)(0)-(24)^(2))/(4(-16))=(-576)/(-64)=9`.

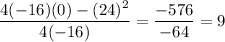∴ Maximum height = 9 ft