Question

Many people think that a national lobby's successful fight against gun control legislation is reflecting the will of a minority of Americans. A previous random sample of 4000 citizens yielded 2250 who are in favor of gun control legislation. How many citizens would need to be sampled if a 99% confidence interval was desired to estimate the true proportion to within 5%?

611



690



653



664

Answer 1

At least 653 citizens need to be sampled.

Explanation:

The following formula is used to compute the minimum sample size required to estimate the true proportion who are in favor of gun control legislation within 5% margin of error:

n≥ p×(1-p) ×
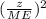`((z)/(ME) )^2` where

• n is the sample size

• p is the sample proportion of people who are in favor of gun control legislation (
  `(2250)/(4000)=0.5625`

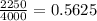
• z is the corresponding z-score for 99% confidence level (2.575)

• ME is the margin of error in the estimation (5% or 0.05)

Putting numbers in the formula

n≥ 0.5625×0.4375 ×
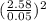`((2.58)/(0.05) )^2` ≈652.7

n needs to be at least 653 to provide this equation.