Answer:
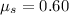
Step-by-step explanation:
It is given that,
Mass of the clock, m = 108 kg
Force acting on it when it is in motion,
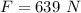
After the clock is in motion, a horizontal force of 521 N keeps it moving with a constant velocity, F' = 521 N
It is assumed to find the coefficient of between the clock and the floor. The force of friction is given by :
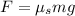
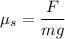
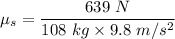
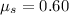
So, the coefficient of static friction between the clock and the floor is 0.6. Hence, this is the required solution.