Answer:
option (C) 22.82 percent
Step-by-step explanation:
Data provided in the question:
Time period, n = 6 years
Annual returns each year: 14%, 9% , 16% , 24%, -40% , 4%
Now,
The average return, Mean =
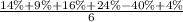
= 4.5%
Standard deviation =
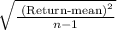
Return (return-mean)²
14 (14-4.5)² =90.25
9 (9-4.5)² =20.25
16 (16-4.5)² =132.25
24 (24-4.5)² =380.25
-40 (-40-4.5)² =1980.25
4 (4-4.5)² =0.25
=========================================
∑(return-mean)² = 2603.5%
Therefore,
Standard deviation =
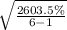
or
Standard deviation = 22.818% ≈ 22.82%
Hence,
The answer is option (C) 22.82 percent