Question

Vector → A has a magnitude of 3.7 units, and vector → B has a magnitude of 11.5 units. If the value of → A ⋅ → B is 22.4 units squared, what is the angle (in degrees) between the two vectors?

Answer 1

`\theta=58.26^(\circ)`

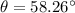
Step-by-step explanation:

It is given that,

Magnitude of vector A,
`|A|=3.7\ units`

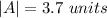
Magnitude of vector B,
`|B|=11.5\ units`

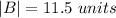
Dot product of two vectors,
`A.B=22.4\ unit^2`

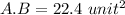
Let
`\theta` is the angle between the two vectors. We know that the angle between two vectors is given by the formula of dot product as :

`A.B=|A||B|\ cos\theta`

`cos\tehta=(A.B)/(|A||B|)`

`cos\tehta=(22.4)/(3.7* 11.5)`

`cos\theta=0.526`

`\theta=58.26^(\circ)`

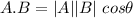
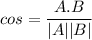
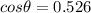
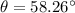
So, the angle between two vectors is 58.26 degrees. Hence, this is the required solution.