Question

The amount of​ carbon-14 present in animal bones after t years is given by ​P(t)equalsUpper P 0 e Superscript negative 0.00012 t. A bone has lost 19​% of its​ carbon-14. How old is the​ bone?

Answer 1

age of bone is 1756 years

Explanation:

The amount of​ carbon-14 present in animal bones after t years

`P(t)= P_0e^(-0.00012t)`

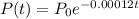
P(t) is the carbon present

19% has lost. so carbon present is 100-19 = 81% present

out of 100 81 is presents

so P0 is 100

P(t) is 81

`81= 100e^(-0.00012t)`

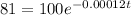
divide by 100 on both sides

`0.81= e^(-0.00012t)`

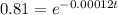
take ln on both sides

`ln(0.081)=-0.00012tln(e)`

`ln(0.081)=-0.00012t`

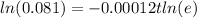
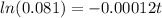
divide both sides by -0.00012

t=1756.0085

age of bone is 1756 years