Question

A bowling ball has a mass of 1.3 kg, a moment of inertia of 0.075088 kg · m2 , and a radius of 0.38 m. It rolls along the lane without slipping at a linear speed of 3 m/s. What is the total kinetic energy of the rolling ball? Answer in units of J.

Answer 1

8.19 Joules

Step-by-step explanation:

m = Mass of ball = 1.3 kg

I = Moment of inertia = 0.075088 kgm²

r = Radius of ball = 0.38 m

v = Linear speed = 3 m/s

Angular speed

`\omega=(v)/(r)`

The linear and rotational kinetic energy will give us the total kinetic energy

`K=(1)/(2)mv^2+(1)/(2)I\omega^2\\\Rightarrow K=(1)/(2)(mv^2+I\omega^2)\\\Rightarrow K=(1)/(2)\left(mv^2+I\left((v)/(r)\right)^2\right)\\\Rightarrow K=(1)/(2)\left(1.3* 3^2+0.075088* \left((3)/(0.38)\right)^2\right)\\\Rightarrow K=8.19\ J`

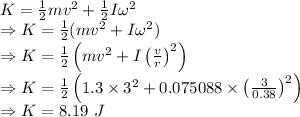
The total kinetic energy of the rolling ball is 8.19 Joules