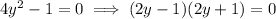Answer:
The given expression is factorized as
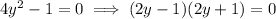
Explanation:
Here, the given expression to factorize is:
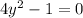
Now, using Algebraic Identity:
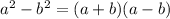
Now here let a = 2y , b = 1
⇒
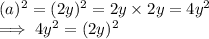
So, The given expression is equivalent to:
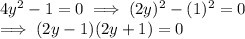
Hence the given expression is factorized as