Question

The length of time for one individual to be served at a cafeteria is a random variable having an exponential distribution with a mean of 77 minutes. What is the probability that a person is served in less than 22 minutes on at least 55 of the next 77 ​days?

Answer 1

0.01265

Explanation:

Since, if the time to be served has an exponential distribution with a mean of 7, then

`P(T < t_0) = 1 - e^{-(t_0)/(7)}`

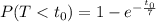
Chance to be served in under 2 minutes:

`P(T<2) = 1-e^{-(2)/(7)} = 0.249`

Let A represents the number of days when a person is served in less than 2 minutes,

Hence,

the probability that a person is served in less than 2 minutes on at least 5 of the next 7 ​days ( using binomial distribution )

= P(A=5) + P(A=6) + P(A=7)

`=^7C_5(0.249)^5(1-0.249)^2+^7C_6(0.249)^6(1-0.249)^1+^7C_7(0.249)^7(1-0.249)^0`

`=(7!)/(2!5!)(0.249)^5(1-0.249)^2+(7!)/(1!6!)(0.249)^6(1-0.249)^1+(7!)/(0!7!)(0.249)^7(1-0.249)^0`

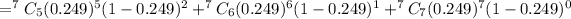
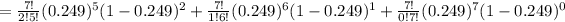
≈ 0.01265