Question

A plane flying with a constant speed of 14 km/min passes over a ground radar station at an altitude of 4 km and climbs at an angle of 45 degrees. At what rate is the distance from the plane to the radar station increasing 3 minutes later?

Answer 1

the rate from the plane to the radar station increasing 3 minutes later is 19.81 km/min

Explanation:

A plane flying with a constant speed of 14 km/min passes over a ground radar station at an altitude of 4 km and climbs at an angle of 45 degrees. At what rate is the distance from the plane to the radar station increasing 3 minutes later?

speed (Δs₁)= change in distance(Δd₁) /(Δt₁)change in time

mathematically,

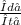`(Δd₁)/(Δt₁)` = Δs₁

= 14 km/min =
`(Δd)/(Δt)`

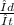
and will are to find the speed after passes the radar

=Δs₂ km/min =
`(Δd₂)/(Δt₂)`

to find d₁ and d₂ with respect to angle 45 degree at 4km

sin 45 = opp/hyp = 4/d₁

d₁ = 4/sin45 = 5.66km

tan 45 == opp/adj = 4/d₂

d₂ =4/tan45 = 4km

for three minute increment,

=3 x d₁ x Δs₁ = 3 x d₂ Δs₂

= 3x5.66x14 = 3x 4 xΔs₂

= 237.72 = 12Δs₂

=Δs₂ = 19.81km/min