Question

On a horizontal frictionless floor, a worker of weight 0.900 kN pushes horizontally with a force of 0.200 kN on a box weighing 1.8 kN. As a result of this push, which statement could be true?

A) The worker will accelerate at 1.08 m/s^2 and the box will accelerate at 2.17 m/s^2, but in opposite directions.
B) The box will not move because the push is less than the weight.
C) The worker and box will bot have an acceleration of 2.17 m/s^2, but in opposite directions.
D) The worker will accelerate at 2.17 m/s^2 and the box will accelerate at 1.08 m/s^2, but in opposite directions.
E)The worker and box will bot have an acceleration of 1.08 m/s^2, but in opposite directions.

Answer 1

D) The worker will accelerate at 2.17 m/s² and the box will accelerate at 1.08 m/s² , but in opposite directions.

Step-by-step explanation:

Newton's third law

Newton's third law or principle of action and reaction states that when two interaction bodies appear equal forces and opposite directions. in each of them.

F₁₂= -F₂₁

F₁₂: Force of the box on the worker

F₂₁: Force of the worker on the box

Newton's second law

∑F = m*a

∑F : algebraic sum of the forces in Newton (N)

m : mass in kilograms (kg)

a : acceleration in meters over second square (m/s²)

Formula to calculate the mass (m)

m = W/g

Where:

W : Weight (N)

g : acceleration due to gravity (m/s²)

Data

W₁ =1.8 kN : box weight

W₂ = 0.900 kN : worker weight

F₂₁ = 0.200 kN

F₁₂ = - 0.200 kN

g = 9.8 m/s²

Newton's second law for the box

∑F = m*a

F₂₁ = m₁*a₁ m₁=W₁/g

0.2 kN = (1.8kN)/(9.8 m/s² ) *a₁

`a_(1) =((0.2kN)*9.8(m)/(s^(2) ) )/(1.8 kN)`

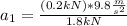
a₁= 1.08 m/s² : acceleration of the box

Newton's second law for the worker

∑F = m*a

F₁₂ = m₂*a₂ , m₂=W₂/g

- 0.2 kN =( (0.9 kN) /(9.8 m/s² ) )*a₂

`a_(1) =((0.2kN)*9.8(m)/(s^(2) ) )/(0.9 kN)`

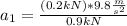
a₂= -2.17 m/s² : acceleration of the worker