Question

A construction worker used 450 N of force to move materials 5 meters in 2 minutes.

How much power did the worker use?
A) 18.75 watts
B) 125 watts
C) 225 watts
Eliminate
D) 1125 watts

Answer 1

The worker used the power of 18.75 watts

Answer: Option A

Explanation:

Power refers the amount of work done in a unit time. So it is directly proportionate to the force exerted to perform a work and inversely proportionate to the time taken to complete the work. Thus if a work is completed within less time, then the power required to do that work is more. The unit of power is watts.

`\text { Power }=\frac{\text {Workdone}}{\text {Time}}`

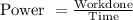
As work done is the amount of force required to complete the work of displacing an object to complete the work.

`\text { Workdone }=\text { Force } * \text { Displacement }`

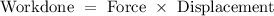
Thus, the equation is

`\text { Power }=\frac{\text { Force } * \text { Displacement }}{\text { Time }}`

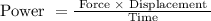
So, by applying given values, we get,

`\text { Power }=\frac{450 \mathrm{N} * 5 \mathrm{m}}{2 * 60 \mathrm{s}}=18.75 \mathrm{watt}`

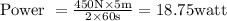
Thus the power required by the worker is 18.75 watts.