Question

A sample is selected from a population with μ = 50, and a treatment is administered to the sample. If the sample variance is s2 = 121, which set of sample characteristics has the greatest likelihood of rejecting the null hypothesis?

a. M = 49 for a sample size of n = 75
b. M = 49 for a sample size of n = 15
c. M = 45 for a sample size of n = 15
d. M = 45 for a sample size of n = 75

Answer 1

The sample d. M = 45 for a sample size of n = 75 has the greatest likelihood of rejecting the null hypothesis.

Explanation:

Greatest likelihood of rejecting the null hypothesis can be found by calculating the z-cores of the sample means. The sample with the biggest absolute z-score value has grater likelihood of rejecting the null hypothesis.

Z-score of the sample means can be calculated as follows:

z=
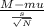`(M-mu)/((s)/(√(N) ) )` where

• M is the sample mean
• μ=mu is the population mean
• s is the standard deviation (square root of variance)
• N is the sample size.

a. M = 49 for a sample size of n = 75

Then z(a)=
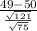`(49-50)/((√(121))/(√(75) ) )` ≈ −0.787

b. M = 49 for a sample size of n = 15

z(b)=
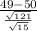`(49-50)/((√(121))/(√(15) ) )` ≈ −0.352

c. M = 45 for a sample size of n = 15

z(c)=
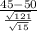`(45-50)/((√(121))/(√(15) ) )` ≈ −1.760

d. M = 45 for a sample size of n = 75

z(d)=
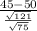`(45-50)/((√(121))/(√(75) ) )` ≈ −3,936

Since z(d) is the lowest, it has the biggest absolute z-value. Therefore sample d is more likely to reject the null hypothesis.