Question

A car traveling east at a constant rate of 33 mi/hr passes through an intersection at 10 A.M. A truck traveling north at a constant rate of 42 mi/hr passes through the same intersection at 11 A.M. If both vehicles maintain their speed and direction, how fast is the distance between them increasing at 1 P.M.?

Answer 1

52.34 miles per hour

Explanation:

Let x represents the distance covered by car and y represents the distance covered by truck,

Also, suppose l represents the distance between them,

∵ car is travelling in east direction while truck is travelling in north direction,

So, by the Pythagoras theorem,

`l^2 = x^2 + y^2----(1)`

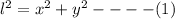
Differentiating with respect to t ( time ),

`2l (dl)/(dt)=2x(dx)/(dt)+3y(dy)/(dt)`

`\implies l (dl)/(dt)=x(dx)/(dt)+y(dy)/(dt)`,

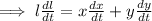Now, the speed of car is 33 mi/hr and speed of truck is 42 mi/hr,

i.e
`(dx)/(dt)=33\text{ mi per hour}\text{ and }(dy)/(dt)=42\text{ mi per hour}`

`\implies l (dl)/(dt)=33x+42y-----(2)`,

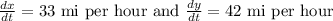
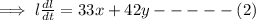Distance = speed × time,

So, y = 42 × 2 = 84 miles,

x = 33 × 3 = 99 miles ( ∵ car travelled 3 hours till 1 PM while truck travelled 2 hours till 1 PM)

From equation (1),

`l = √(84^2 + 99^2)=√(7056+9801)=√(16857)=129.83`

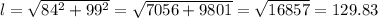
From equation (2),

`129.83(dl)/(dt)=33(99)+42(84) = 3267+3528=6795`

`\implies (dl)/(dt)=(6795)/(129.83)=52.34\text{ miles per hour}`

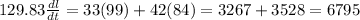
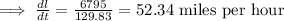
Hence, the distance between them is increasing by 52.34 miles per hour.

Answer 2

Answer:52.33 m/s

Explanation:

Given

Speed of car
`v_1=33 mi/hr`

Speed of truck
`v_2=42 mi/hr`

Distance traveled by car in 1 hr is 33 mi

Therefore after 11 am distance of car and truck from Junction in time t is

Car
`=33+33t`

truck
`=42 t`

Let D be the distance between them

`D^2=42t^2+(33+33t)^2`------------1

at
`t= 2 hr`

`D^2=(42* 2)^2+(33+66)^2`

`D=129.83 miles`

To get how fast distance between them is increasing differentiate 1 we get

`2D\frac{\mathrm{d} D}{\mathrm{d} t}=2\cdot(42)^2t+2\cdot 33^2(1+t)`

`\frac{\mathrm{d} D}{\mathrm{d} t}=(42^2t+33^2\left ( 1+t\right ))/(D)`

`\frac{\mathrm{d} D}{\mathrm{d} t}=(1764* 2+1089* 3)/(D)`

`\frac{\mathrm{d} D}{\mathrm{d} t}=(6795)/(129.83)=52.33 m/s`