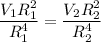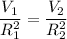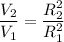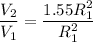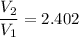Question

Two hoses are connected to the same outlet using a Y-connector, as the drawing shows. The hoses A and B have the same length, but hose B has the larger radius. Each is open to the atmosphere at the end where the water exits. Water flows through both hoses as a viscous fluid, and Poiseuille's law

Q =πR4(P2 − P1)
8ηL applies to each. In this law, P2 is the pressure upstream, P1 is the pressure downstream, and Q is the volume flow rate. The ratio of the radius of hose B to the radius of hose A is RB/RA = 1.55. Find the ratio of the speed of the water in hose B to the speed in hose A.
vB/vA=

Answer 1

`(V_2)/(V_1)=2.402`

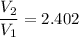
Step-by-step explanation:

Given that

Lets take radius of pipe A = R₁

Lets take radius of pipe B = R₂

R₂/R₁ = 1.55

These pipes are connected in the parallel connection that is why pressure difference will be same

`Q=(\pi R^4\Delta P)/(8\eta L)`

`\Delta P=(8\eta LQ)/(\pi R^4){}`

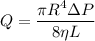
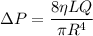
Given that length of both the pipes is same

So we can say that

`(Q_1)/(R_1^4)=(Q_2)/(R_2^4)`

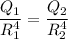
We know that

Q= A V

A= Area

V= velocity

A=π R²

So we can say that

`(V_1R_1^2)/(R_1^4)=(V_2R_2^2)/(R_2^4)`

`(V_1)/(R_1^2)=(V_2)/(R_2^2)`

`(V_1)/(V_2)=(R_1^2)/(R_2^2)`

`(V_2)/(V_1)=(R_2^2)/(R_1^2)`

`(V_2)/(V_1)=(1.55R_1^2)/(R_1^2)`

`(V_2)/(V_1)=2.402`