Question

Discuss all possible scenarios for the Discriminant when solving a Quadratic equation using Quadratic formula? Give an example.

Answer 1

Step-by-step explanation:

For a quadratic equation in standard form with real coefficients:

`ax^2+bx+c=0`

The quadratic formula giving its solutions is ...

`x=(-b\pm√(b^2-4ac))/(2a)`

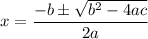
The quantity under the radical is called the discriminant. If we let d represent it, then ...

d = b²-4ac

and there are three possibilities:

1. d < 0. The solutions involve the square root of a negative number, so both are complex. They are conjugates of each other.
2. d = 0. There is one real solution. It has multiplicity 2.
3. d > 0. There are two distinct real roots.

If the coefficients of the quadratic are rational, the roots will be irrational if and only if d is not a perfect square.

_____

The above formula still applies when coefficients are complex or irrational (or both). In the case of complex coefficients, the description of the number of roots is accurate, but their description as real or complex may not apply.

_____

Examples:

(x -1)² +1 = 0 = x² -2x +2 . . . . d = (-2)²-4(1)(2) = -4; roots are x = 1 ± i

(x-2)² = 0 = x² -4x +4 . . . . . . d = (-4)² -4(1)(4) = 0; roots are x = 2 (twice)

(x+3)² -4 = x² +6x +5 . . . . . . d = 6² -4(1)(5) = 16; roots are x = -5 and x = -1