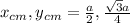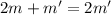Answer:Twice of given mass
Step-by-step explanation:
Given
Two Particles of Equal mass placed at the base of an equilateral Triangle
let mass of two equal masses be m and third mass be m'
Taking one of the masses at origin
Therefore co-ordinates of first mass be (0,0)
Co-ordinates of other equal mass is (a,0)
if a is the length of triangle
co-ordinates of final mass
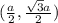
Given its center of mass is at midway between base and third vertex therefore