Question

Randy presses RAND on his calculator twice to obtain two random numbers between 0 and 1. Let $p$ be the probability that these two numbers and 1 form the sides of an obtuse triangle. Find $4p$.

Answer 1

pi - 2 would be the answer to AoPs.

Answer 2

`(\pi)/(4)`

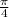
Explanation:

Lets call x,y the numbers we obtain from the calculator. x and y are independent random variables of uniform[0,1] distribution.

Lets note that, since both x and y are between 0 and 1, then 1 is the biggest side of the triangle.

Lets first make a geometric interpretation. If the triangle were to be rectangle, then the side of lenght 1 should be its hypotenuse, and therefore x and y should satisfy this property:

x²+y² = 1

Remember that in this case we are supposing the triangle to be rectangle. But the exercise asks us to obtain an obtuse triangle. For that we will need to increase the angle obtained by the sides of lenght x and y. We can do that by 'expanding' the triangle, but if we do that preserving the values of x and y, then the side of lenght 1 should increase its lenght, which we dont want to. Thus, if we expand the triangle then we should also reduce the value of x and/or y so that the side of lenght 1 could preserve its lenght. With this intuition we could deduce that

x²+y² < 1

Now lets do a more mathematical approach. According to the Cosine theorem, a triangle of three sides of lenght a,b,c satisfies

a² = b²+c² - 2bc* cos(α), where α is the angle between the sides of lenght b and c.

Aplying this formula to our triangle, we have that

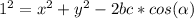`1^2 = x^2 + y^2 - 2bc* cos(\alpha)` , where
`\alpha` is the angle between the sides of lenght x and y.

Since the triangle is obtuse, then
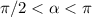`\pi/2 <  \alpha < \pi` , and for those values
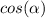`cos(\alpha)` is negative , hence we also obtain

1 > x² + y²

Thus, we need to calculate P(x²+y² <1). This probability can be calculated throught integration. We need to use polar coordinates.

(x, y) = (r*cosФ,r*senФ)

Where r is between 0 and 1, and Ф is between 0 and
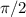`\pi /2` (that way, the numbers are positive).

The jacobian matrix has determinant r, therefore,

`{\int\int}\limits_(x^2+y^2 < 1)  \, dxdy = \int\limits^1_0\int\limits^{(\pi)/(2)}_0 {r} \, d\phi dr = (\pi)/(2) * \int\limits^1_0 {r} \, dr =    (\pi)/(2) * ((r^2)/(2) |^1_0) = (\pi)/(4)`

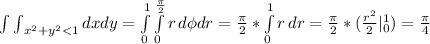
As a conclusion, the probability of obtaining an obtuse triangle is
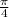`(\pi)/(4)` .