Answer:
First Term:
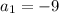
Common Difference : d= 4
Recursive formula:
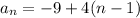
Explanation:
Here we are going to use the arithmetic progression formula:
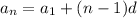
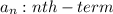
d :common difference
Since we are given the 5th term and 19th term, we can write them as :
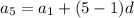
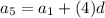
as
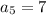
so,
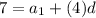 -------------------(Equation 1)
-------------------(Equation 1)
Moreover, using same formula for 19th term
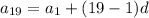
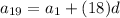
As

So,
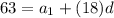 --------------------(Equation 2)
--------------------(Equation 2)
From Equation 1, we have:

put the value in equation 2:
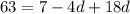
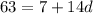
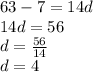
Which is the common difference
Now put the value of d in equation 1:
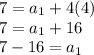
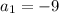
Which is the first term
Putting the firm term and common difference in the initial arithmetic progression formula:
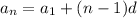
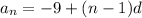
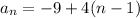
Which is the recursive formula of the sequence