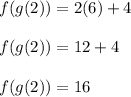Answer:
Explanation:
Given the function
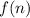 :
:
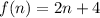
And the function
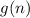 :
:

The first step we can apply is to find
 . To do it, we need to substitute
. To do it, we need to substitute
 into the function and then we must evalute. Then, this is:
into the function and then we must evalute. Then, this is:
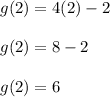
Finally, in order to find
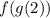 we need to substitute
we need to substitute
 found above, into the function
found above, into the function
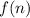 and then we must evaluate.
and then we must evaluate.
So, we get: