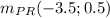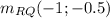Answer:
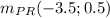
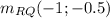
Explanation:
The midsegment that is being asks has endpoints on PR and RQ, exactly from midpoint of one side to the midpoint of the other side.
So, to find the coordinates of this midsegment, we just have to find the mid point between PR and RQ.

Therefore the midsegment starts at
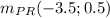
Now, we calculate the other coordinate, which is the mid point of RQ:
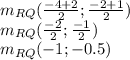
Therefore, the endpoint coordinates for the midsegment are: