Answer:
 ,
,
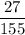 , and
, and
 .
.
Explanation:
What is a rational number? By definition, a rational number can be represented as the fraction of two integers.
The goal is to find three fractions in the form
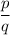 between
between
 and
and
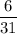 .
.
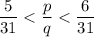 .
.
At this moment, there doesn't seems to be a number that could fit. The question is asking for three of these numbers. Multiple the numerator and the denominator by a number greater than three (e.g., five) to obtain
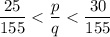 .
.
Since
 and
and
 can be any integers, let
can be any integers, let
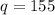 .
.
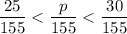 .
.
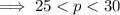 .
.
Possible values of
 are 26, 27, and 28. That corresponds to the fractions
are 26, 27, and 28. That corresponds to the fractions
 ,
,
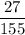 , and
, and
 .
.
These are all rational numbers for they are fractions of integers.