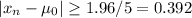Answer:
c=0.392
Explanation:
Given that X1,...,Xn form a random sample from the normal distribution with unknown mean μ and known variance 1.
Suppose also that μ0 is a certain specified number, and that the following hypotheses are to be tested:
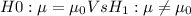
This is two tailed test.
Alpha =0.05
Sample size = 25
we reject null hypothesis if
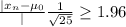
Or