Question

The y-axis on a distance-time graph would be ____________. time distance speed

Answer 1

Answer:its distance

Step-by-step explanation:

Answer 2

The y-axis on a distance-time graph would be distance.

Answer: Option B

Explanation:

It is known that velocity can be derived from the distance-time graph. And also time is the independent variable among the distance and time. As based on time taken we have to calculate the covered distance. So the independent variable should be placed in x-axis and dependent variable usually is written in the y-axis. Hence distance covered is a function of time.

It is also known that slope of the line obtained in distance-time graph will help in obtaining the velocity and slope in any graph is calculated as the ratio of y-axis points to x-axis points. So if we compare it with the general definition for velocity, the slope of the graph should be equal to ratio of distance to time. It can express as below:

`\text {velocity}=\frac{\text {Distance covered}}{\text {Time interval}}`

From the distance-time graph,

`\text {velocity}=\text {slope of the graph}=(y_(f)-y_(i))/(x_(f)-x_(i))`

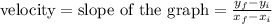
Thus, if we compare both,

`\text {velocity}=\frac{\text {Distance covered}}{\text {Time interval}}=\text {Slope of graph}`

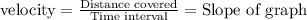
So,

`\text {velocity}=\frac{\text {Distance covered}}{\text {Time interval}}=(y_(f)-y_(i))/(x_(f)-x_(i))`

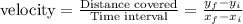
Hence it gets confirmed that y-axis on distance-time graph would be distance only.