Question

Suppose that a 2M x 16 main memory is built using 256K x 8 RAM chips and memory is word addressable.a) How many RAM chips are necessary?b) If we were accessing one full word, how many chips would be involved?c) How many address bits are needed for each RAM chip?d) How many banks will this memory have?e) How many address bits are needed for all memory?f) If high-order interleaving is used, where would address 14 (which is E in hex) be located?9) Repeat exercise 9f for low-order interleaving

Answer 1

(a) 16 RAM chips

(b) 2 chips

(c) 18 address bits

(d) 8 banks

(e) 21 bits

(f) 0000

(g) 1110

Step-by-step explanation:

(a)

The number of RAM chips necessary are found by dividing memory size by chip size. Here, the memory size is

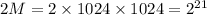`2M=2* 1024* 1024=2^(21)` by
`16=2^(4)`

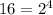
Chips size is
`256K=256*1024=2^(18)` by
`8=2^(3)`

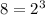
Therefore, RAM needed is
`\frac {2M* 16}{256K * 8}=\frac {2^(21) * 2^(4)}{2^(18) * 2^(3)}=2^(4)=16`

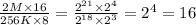
Therefore, 16 RAM chips of
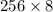`256* 8` are needed to obtain main memory of
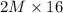`2M* 16`. This can further be arranged in 8 rows and 2 columns each

(b)

The RAM chips holds 8 bits or 1 byte for addressable word while main memory holds 16 bits or 2 bytes. Since the design needs 16 bit word, the first chip holds the high-order byte of the word and second chip holds the low-order byte of the word. Therefore, 2 chips would be involved to access one word

(c)

For
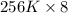`256K* 8` RAM chip, bits required are
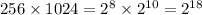`256* 1024=2^(8)* 2^(10)=2^(18)` hence 18 address bits needed for each RAM chip

(d)

The number of addressable items in the main memory and chips determine the number of modules

The number of modules or banks is given by dividing main memory addressable items by addressable items in chips

Therefore,
`banks=\frac {2M}{256K}=\frac {2*1024* 1024}{256* 1024}=\frac {2^(21)}{2^(18)}=2^(3)=8`

Therefore, number of banks equals 8

(e)

Bits required for main memory is
`2M=2* 1024* 1024=2* 2^(10)* 2^(10)=2^(21)`

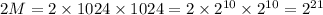
Therefore, 21 bits are needed to address main memory. To prove, part c required 18 bits for RAM chip leaving 21-8=3 bits to select the bank we have therefore
`2^(3)=8` banks in part d hence everything is okay

(f)

Normally, the high order memory interleaving distributes the address in a way that each bank has consecutive addresses. Here, the first 256 K words goes to bank 0 and so the address 14 will also be in the same bank. If high-order memory is used, address 14 (E in hexadecimal) is found in bank 0(000 in decimal)

(g)

From part e we found 21 address bits which will be labelled
`A_0-A_(20)`

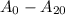
Low-order interleaved memory places addresses of memory in different memory banks. Here, address 14 is 0xE in hexadecimal and in 1110 in binary. Therefore, for address 14, the bank is binary 110 as illustrated in the attached image.